美國國庫券小數學 – 2

上次寫那篇主要是因為 AI 出錯, 引發了我想記錄下來的興趣. 但後來看到一些類題需要腦筋再多轉幾個彎. 我還是做個筆記才好複習.

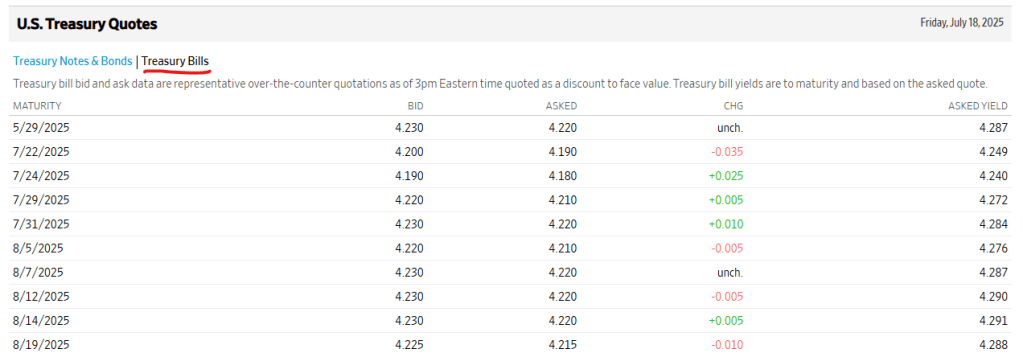
Q1, 有個 T-Bills 用 99,900 買了, 還有 180 天到期. yield to maturity 是多少?

上回講到計算隱含價值, 這回我買都買了, 狀況就不一樣. 所以不是用那個公式, 倒是可以用直覺.

由於 180 天後我可以拿到 100,000 元, 表示我可以賺 100,000 – 99,900 = 100 (元).

獲利率 = 100/99,900, 後續可以當作 Annual Payment Rate = APR 來計算.

年化 yield to maturity = 100/99,900 x (360/180) = 0.2002%

Q2. EAR 是多少?

Effective Annual Rate = EAR = (1 + APR/m)m , 本例子中, 我剛好買在生命周期的一半, 故兩個半年相當於兩期, m = 2.

EAR = (1 + 0.1001%)360/180 – 1 = 0.2003%

這明顯是一個買貴的例子. 但注意 EAR 只會比 yield to maturity 大一點點. 如果數量級差太多就是算錯了.

Q3. 隔夜逆回購 (ON RRP = Over Night Reverse Repurchase)

A 銀行在美聯儲的存款帳戶（reserve account）有閒置的 10 億美金, 向美聯儲申請參與 ON RRP, 假設隔夜逆回購利率 5.8%, 1 天能賺到多少錢?

美聯儲接受 ON RRP 申請後, 銀行將指示美聯儲從自己在聯儲的帳戶扣款 (減少 reserve balance), 當作國債的抵押品. 銀行則得到國債一紙.

第二天, 美聯儲把錢還給銀行, 並且支付國債利息  10億美元 * 5.80% * (1/360) ≒ 16.11 萬美元. A 銀行把國債還給美聯儲.

假設匯率 1 USD = 29.49, TWD, 16.11 萬美元 = 475.1 萬元台幣.

參考 [1], 銀行不勞而獲的結果, 剛好可以養一個螃蟹工程師 (對, 數字我湊的). 我的重點是, 錢每天都在貶值, 你怎麼可以不投資?

[REF]

  1. https://news.tvbs.com.tw/life/2889863

美國國庫券小數學

美國國庫券 (Treasury Bills, T-Bills) 價錢怎麼算呢? 其實很簡單, 但是要計算天數. 我本來想把這個惱人的事情給 AI 做, 想不到最近數學大有進步的 AI 竟然就瘋了?

[ 3 + 31 + 30 + 31 + 30 + 31 + 31 + 28 + 30 = 3 + 31 + 30 + 31 + 30 + 31 + 31 + 28 + 30 = 3 + 31 + 30 + 31 + 30 + 31 + 31 + 28 + 30 = 3 + 31 + 30 + 31 + 30 + 31 + 31 + 28 + 30 = 3 + 31 + 30 + 31 + 30 + 31 + 31 + 28 + 30 = 3 + 31 + 30 + 31 + 30 + 31 + 31 + 28 + 30 = 3 + 31 + 30 + 31 + 30 + 31 + 31 + 28 + 30 = 3 + 31 + 30 + 31 + 30 + 31 + 31 + 28 + 30 = 3 + 31 + 30 + 31 + 30 + 31 + 31 + 28 + 30 = 3 + 31 + 30 + 31 + 30 + 31 + 31 + 28 + 30 = 3 + 31 + 30 + 31 + 30 + 31 + 31 + 28 + 30 = 3 + 31 + 30 + 31 + 30 + 31 + 31 + 28 + 30 = 3 + 31 + 30 + 31 + 30 + 31 + 31 + 28 + 30 = 3 + 31 + 30 + 31 +…. 後面塞爆自動停了.

我只好自己把上面加起來, 以利息來算, 經過 244 天.

Bo = FaceVelue * (1 – d * D / 360), 其中

FaceValue = 面值

d= 折扣率 = discount quote (%),

D = 到期日 = day to mature (貨幣市場都小於一年)

360 = 約定俗成的一年天數

Bo = 隱含價格

Discount quote 是什麼呢? 根據報價網站 [1],我們可以看到 US Treasury Quotes 的數據. 記得要選到 Treasure Bills (下圖紅色畫底線), 另外一邊是 Treasury Notes.

其中, bid (買價) 和 asked (賣價) 都是 discount quote. 所以會算出兩個隱含價值. 在網路課程中, 舉的 discount 都是 0.4%, 過了七八年, discount 已經變成 4% 了!

利率變高好像沒有什麼大不了的, 債券利率也很明顯比以前變高啊! But, 債券是有債息的, 國庫券根本不配息, 它只有面值. 只會透過低於面值的折扣價來買賣.

舉例來說, 美聯儲發行 Treasure Bills 讓銀行買, 銀行用折扣價買入, 準備賺個年利率 5%. 當銀行現金不足, 可以把 T-Bills 賣給別的銀行周轉. 這個流動性是債券所沒有的, 因為它一年之內就會到期, 等同自帶 timer 的現金.

若是經濟不好的時候, 美國不用發現金、不用發 5 倍劵, 而是加價買回市場上的 T-Bills. 因為銀行就是賺錢機器, 在利益優先的考慮之下, 就自動成了美聯儲的打手, 喔不, 推手. 當銀行變得滿手現金, 自然就會想要用它賺更多錢, 也就間接刺激了市場成長. 當然這是最理想的狀況. 等我學成之後, 應該可以舉出很多歪樓的狀況.

[REF]

  1. https://www.wsj.com/market-data/bonds/treasuries

買賣債券小數學

purchased a 15-year bond that pays semi-annual coupon of $20 and is currently selling at par. What would your realized annual return be if you sold the bond five years later when the yield is 5.5%?

這題看起來很短, 但是足夠複習一些知識了.

原本大家都想知道美國降息之後, 債券會漲多少? 這題剛好相反, 是問上升後, 逢高賣出可賺多少? 我們要先知道賣出的合理價錢. 也就是 5 年後的 Pv . 會讓我腦筋打結的地方是要從 15 年後回推 5 年後, 所以是 10 年期間, 半年配息一次, 共 20 個週期. 假設面值 1,000.

Pv = 20 * ADF(5.5%/2, 20) + 1,000 / (1+5.5%/2)^20

上回筆記到 Annual Discount Factor = ADF(r, n) = (1−(1+r)-n)/r

因此在利率上漲到 5.5% 時, 該債券值 885.7956. 此處假設未來第 6~15 年利率都是 5.5%.

因為是按照面值買的 (at par), 所以我的成本是 1,000. 最後價值是 885.8, 求年報酬率 g, 半年是 g/2.

1000 = 20 * ADF(g/2, 10) + 885.7956 / (1+g/2)^10

沒有財務計算機就用 Excel. 其中 905.8 = 885.8 + 20, 最後一年是本利合計.

g/2 =IRR([-1000, 20, 20, 20, 20, 20, 20, 20, 20, 20, 905.80])

解出 g = 1.807%.

知道這個技巧後, 換個場景.

20 年美債, 面值 1000 元, 殖利率 5%, 半年配, 以現值 Pv = ADF(5%/2, 40) + 1,000 / (1+5%/2)^40 = 1000 合理價買入.

買了持有 5 年, 利率果真降到 3%, 此時債券價值上漲為 1240.158 . 公式跟上面都一樣.

Pv = 1240.158 = 20 * ADF(3%/2, 30) + 1,000 / (1+3%/2)^30

這段期間的 IRR([-1000.39, 25, 25, 25, 25, 25, 25, 25, 25, 25, 1240.158+25]) = 4.45%

整年 = 半年 * 2 = 8.9%.

假如債券殖利率真的這樣發展, 跟每年台灣大盤的平均漲幅也差不多. 但抱得愈久, 或是殖利率跌得愈少, 就會輸給大盤. 當然在台灣買, 還有匯率變動問題. 因此買長債這個送分題只有邏輯正確, 川普都想讓你賺, 但這次時間之神還沒同意.

2025 年 Q2 投資回顧

先講結果, Q2 整體投資淨值比 2024 年底低了 0.78%, 但已經比 Q1 好上 0.76%, 差不多就是這兩個時間點的平均值. 換言之, 算是連滾帶爬地救回了一半.

雖然美股那邊已經回到高點, 甚至創新高. 但是拜台幣半年升值 10.69% 之賜, 我的投資組合漲得不如匯率跌得兇, 故還在虧損階段.

2024/12/31~2025/6/30 的投資淨值, 就以貝里幣示意如下.

相較於 2025 年 Q1 的規劃是去除雜質, 我在 Q2 沒有什麼大動作. 主要就是用定期定額買 QQQ 和 PFF. 作為雜質代表的 KO, 成了我想賣又捨不得賣的懸念.

要賣掉 KO 當然是選個股價高點. 但很可惜地現在卻是匯率低點. 我的 KO 是用台幣複委託買的, 不要說有沒有創新高了, 現在賣掉就現虧 10% 匯損. 我看我同事 (Ri)2 這幾週開會都不喝可樂了,與其等待 KO 股價再漲 10%, 還不如期待美元指數周期性的輪動來得實在.

因為 QQQ 買了又買, 現在它已經佔我的投資組合一半以上了.

這半年來確實有考慮買一些歐洲的 ETF, 像是 VGK. 因為台幣兌歐元也明顯升值, 歐股相對是便宜價. 不過一來現在閒錢不太夠用, 不知道要賣誰來換比較好? 二來是考慮到穩定收益對我更重要, 所以沒有實際做出投資.

說到穩定收益, 目前主要靠 PFF 和 SHEL 的配息. PFF 的股價有點下跌, 從近期高點下滑 8.66%. 不過這個表現還是比美債 20 年 ETF 那些好一倍 (抓元大美債 20 年 ETF 的話, 大約是掉了 17.3%). SHEL 股價距離最高點掉了 5.44%, 我認為這屬於正常波動範圍, 可以接受.

同樣都是石油股, 巴西石油 (PBR) 的各項指標似乎都比殼牌好 [1]. 不過再怎麼說, 我對殼牌的信心還是高一點. 我不太能想像以後要靠巴西人賺退休金的情境.

講到退休, 常常聽到只要存一筆錢, 每年提領 4% 就好這種論調. 或者反推現在每年要用多少錢, 就要準備 25 倍於那個數字. 然而, 其實賺多少和花多少不一定會連動, 還是跟個人生活型態有關. 如果本來花錢就大手大腳, 退休後只能綁手綁腳, 那餘生的心情一定都很糟. 除非自己是個自我 PUA 的大師~~~

像我們家那麼窮, 問題就不大. 只要退休後的所得替代率還過得去, 我在退休前後都可以保持我的生活樣貌. 我心目中的所得替代率共有兩個, 分別對應月薪和年薪. 以下都是考慮稅後的數字.

(1) 月薪版: 股債配息 + 勞退/勞保年金 vs 月薪 + 公提金

(2) 年薪版: 每年總資產淨值成長幅度 vs 年薪

原本在 Q1 的時候, 我就很開心地達到了月薪替代率 90%. 但人算不如天算, 美金貶值後月薪替代率就只剩下 81.83 %. 這表示如果退休了, 麥當勞只能點小薯、中可, 所幸還是能吃到大麥克.

至於年薪方面, 過去 12 年累積投資獲利是年薪總和的 1.94 倍. 雖然開頭幾個年頭比較多次低於 100%, 但是從來沒有變成負數過. 基本上, 股息再投入的全市場投資是複利計算, 即使獲利率不變, 期望值也會愈來愈大. 只有變異數無法預知, 畢竟高低起伏在所難免.

而每年的年薪都是獨立事件, 有高有低, 更不可能連續暴漲. 照理說, 長期下來薪水這方就會逐漸被投資拋開才對. However, 這是兩個隨機變數之間的比較, 目前投資這邊雖然輸了. 但樂觀來說, 今年還剩下一半. 讓我們拭目以待整年度的成果如何吧?

即使 2025 年真的成為台幣計價的美股荒年, 今年過了還有明年. 明年過了還有後年,… 長期來說, 持續投資全市場應該輸不了! 雖然我不是經濟學家, 也不是預言家. 我相信事情應該是如此發展. 萬一不是這樣呢, 也頂多是以後改吃小薯小可加上吉士堡而已, 問題不大. 更何況, 萬一2025/7/5 就是世界末日 [2], 想那麼多也沒用不是嗎? 哈!

[REF]

  1. PBR与SHEL：股票综合比较
  2. https://esg.gvm.com.tw/article/85276

資產小筆記

資產可以分為金融資產 (financial assets) 和實物資產 (real assets) 兩類. 實物資產的價值就是它的現值, 金融資產考慮的是它未來的價值折現後的現值.

Peter Bernstein 說 “Financial Markets are a kind of time machine that allows selling investors to compress the future into the present and buying investors to stretch the present into the future."

[按照請求權是否固定分類]

金融資產又分為 fixed amount claim (固定金額請求權) 和 residual or equity claim (剩餘或股權請求權). “claim"指的是投資者對金融資產的請求權或所有權.

“固定金額的 claim" 代表投資者擁有固定的本金和收益, 例如買了債券, 就會收到固定的利息.

“剩餘或股權的 claim" 表示投資者的收益取決於公司的經營狀況, 例如買了股票, 公司賺得多就分得多. 優先股有債券性質, 但還是跟股票分在一類.

[按照到期日長短分類]

金融市場又分為貨幣市場 (money market) 和資本市場 (capital market).

一年以內到期的債券屬於 money market, 超過一年期的債券和股票 (含優先股) 屬於 capital market.

所以, 巴菲特買一年期國債, 是從資本市場撤到貨幣市場. 對金融市場來說, 竟然超過一年就算是長期投資. 真是有點驚訝!

[REF]

  1. https://xueqiu.com/1383267494/132605480