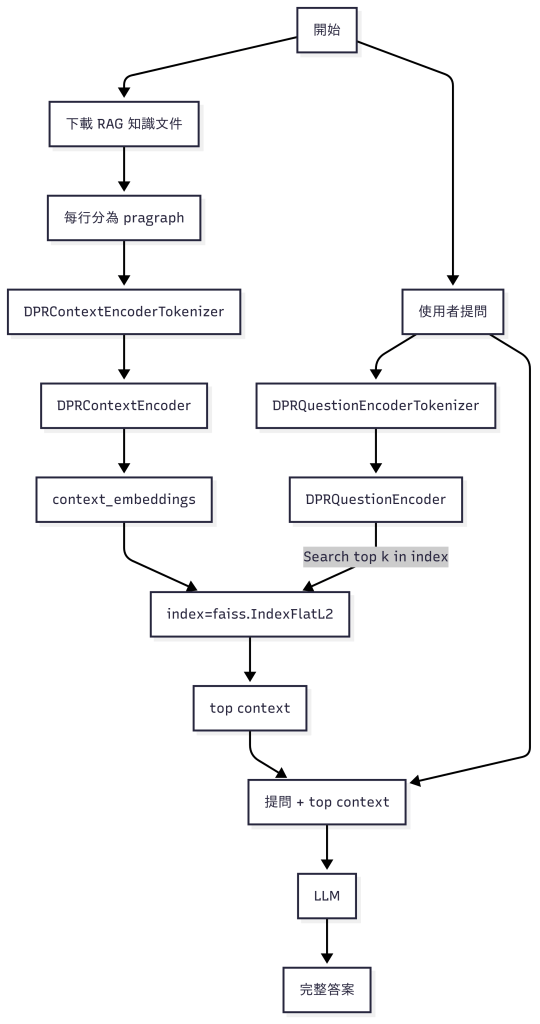
Atomic Habits – 本書的作者是詹姆斯克里爾 (James Clear),我讀的版本是蔡仕偉先生翻譯,方智出版社發行。作者能夠跟大家談習慣養成的底氣在於親身的經歷。高二那年在棒球賽中,他被同學甩棒打中門面,造成骨折、複視、癲癇…等傷害,幾乎斷送運動生命。然而六年後,他在大四成為 ESPN 全明星隊投手、總統獎章得主。這個艱苦的復健過程,應證了養成好習慣並持之以恆的可能性。
好習慣的養成有四個法則 – 類似管理上的 PDCA [1] 這樣反覆加強,分別是提示、渴望、回應、獎賞 (cue, craving, response, and reward)。渴望這個詞,我理解為渴求;不然太文謅謅了,其實就是 “想要" 某個東西。擴充幾句就是: (1) 提示一個目標,(2) 激起達到目標的渴望,(3) 做出能達到目標的某件事,(4) 並獲得獎賞。
習慣的緣起是很細微的事情,所以作者才會用 atomic 來描述它。而習慣造成的影響剛開始可能影響微小,像是冰塊加熱到 0 度才突然變成水,竹子雨後突然爆長,甚至只要六週就長到 90 英呎高 (p.18~p.19)。以前國文課讀過劉蓉的 «習慣說»,大家也都知道 “習慣成自然" 這個成語。它說明好習慣也會有一段沒有回報的潛伏期 (p.19),假設大家都能接受這件事,就可以減少一些挫折感。像是運動了好幾週也沒變瘦。
在上面的論述中,作者已經悄悄地把習慣養成和目標設定做了聯結。這本書不只是要教大家怎麼養成好習慣,而是要講如何達成目標。通常我們會為自己訂目標,做出規劃,然後進入需要反覆操作的階段,順便在不知不覺中獲得一些好習慣。例如為了準備考試,早上 6 點起床讀書。或者我們了解到某些好習慣對身體有益無害,例如每週運動三次。於是作者認為與其緊盯著偉大的目標,不如堅持過程 (process),靠著不斷進步 (progress) 去達成它 (p.21)。
擴大而言,我們完成目標需要一套系統,這個系統有目標也有過程。例如目標是職棒年度總冠軍,我們要拆解系統成為可以回饋的子系統,如果只有大目標,卻沒有建立系統,並不一定會成功。因為,你的對手的目標跟你一模一樣 (p.20),為什麼偏偏是你奪冠呢? 顯然大家對於系統的設計就有不同的看法,然後才是比執行力,以及能否堅持到成為一種習慣。
作者舉出反例說,假如我們眼裡只有目標,大目標前面放個中目標,例如先得個上半季冠軍吧! 球隊可能也真的做到了,但是下半季發生溜溜球效應 [3],球隊忽然失去打球的動力,結果離目標更遠。我想富邦悍將或許是把熱身賽得第一當作小目標吧,以至於每年都第一個被淘汰!? 哈!
作者說大目標只是你想要改變的結果。深入一層去看,你應該要改變過程。再更深入地去理解,則是你要改變身分認同 – 你心裡希望成為什麼樣的人 (p. 23)。有人遞菸給甲,甲說我在戒菸;遞給乙,乙說我不抽菸。甲是個正在戒菸的人,乙是個已經戒菸的人 (或者從不抽菸)。作者舉這個例子說明身分認同是什麼? 我們的行動代表一個信念系統,有信仰可以讓習慣更持久。習慣也讓你成為理想的自己。
這四個法則都有正反兩面,既可以做正向加強、並做負向削減。例如:我們讓養成好習慣的物件顯而易見、讓養成壞習慣的物件隱而不見。假設想戒菸,就最好整天都看不到菸 (讓提示隱而不顯);想要讀書,書就放在垂手可得的地方 (讓提示顯而易見) (p. 33)。或者說,環境、情境比激勵更重要 (p. 44)。這也解釋了為何孟母要三遷,人類在新環境中比較容易改變習慣,戒毒也是如此 (p. 47)。還有模仿的對象也很重要 (p. 57)。
要提升自己,就要注意自己已經感覺不到的習慣是好是壞? 然後決定保持或是戒掉。書上說從一早開始做了哪些事? 可以詳細記錄 “習慣計分卡" 來做檢查 (p. 37, p. 89)。至於要養成一個好習慣,除了明確知道要做什麼,還要知道何時何地去做。例如自己宣告要在某個時間地點運動,執行力比只決定要運動好 2 倍以上 (p. 39)。
好習慣還可以疊加,造成鏈結。例如每次做完 A 之後,就固定做 B。習慣 A –>B 之後,可以在培養 B –> C 的習慣,這樣每件事都暗示著下一件事,整個生活都可以步上新的軌道 (p. 40)。
改變行為的第二條法則在於讓習慣有吸引力 (p. 52)。多巴胺測量實驗證明,想到快要達成目標的感覺比實際達成目標時更快樂! 所以想要 (craving) 的感覺可以幫助我們養成習慣。作者說我們可以綁定獎賞和一個待養成的好習慣,例如拿出手機就先做十下波比跳 [4] (需要) 再看臉書 (想要)。至於要戒掉壞習慣,就是要讓它變得毫無吸引力 (p.63)。
既然是習慣,養成的重點在於重複,而不是完美 (p. 66)。例如寫日記或是 Youtube 日更這種習慣。行為改變的第三法則是讓行動變得輕而易舉 (p. 70)。書上說農業技術的傳播對於同個緯度的地區比較容易,因此東西向傳播很快,但南北向傳遞速度只有 1/2~1/3。
追求輕鬆,最小努力是人類的本能,在每個決定性的瞬間我們要讓環境引導我們自然而然選擇好習慣,想都不用想 (p.75)。為了瞬間可以做出好的選擇,我們的目標可以定在 2 分鐘就可以做到的小段落。像是每晚就寢前讀書,先簡化為讀一頁就好 (p. 77)。
再來談到獎賞。眾所周知,重賞之下必有勇夫,而且即時獎勵效果更好 (p. 86)。這對別人適用,對自己也適用。特別值得一提的是 – 作者說父母鼓勵小孩時,可以給予代幣 (星星或其他的 token),讓小孩受到正向的鼓勵。在小孩做錯事情,例如說髒話,優先冷處理,輕描淡寫地說 “那樣說話不好。" 而不是去扣掉他的代幣或是劃掉小星星,因為負向的增強也是增強 (p. 128~p.129),衝擊到價值觀的純淨性。或許此時可以給一道閃電做出區隔 [5]。
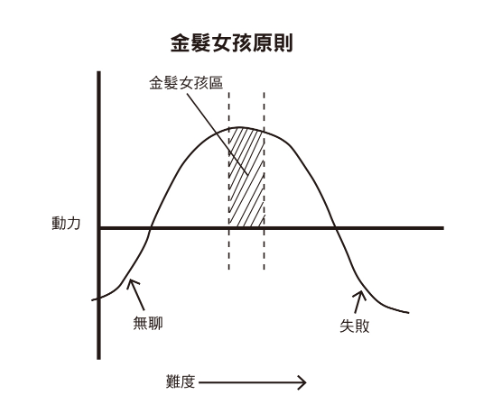
本書在第 18 章有一記回馬槍,提到基因影響習慣 (p. 97)。不要違反你的天賦去培養沒好處的習慣,例如長不高想打籃球、虎背熊腰去跑馬拉松之類的 。第 19 章也稍微有點歪樓 (p. 100)。它說要在生活與工作中維持動力,只要求達到剛好難度的目標,否則培養 CP 值很低的習慣也沒有好處。書上提到這個金髮女孩原則,就是小時候讀的金捲兒闖入三隻熊家裡偷吃東西、偷睡床鋪的那個故事。當小偷還要挑三揀四選剛剛好的。
第 20 章回頭講養成好習慣的潛伏期 (p.104),只是更強調心理建設。書上說我們要對自己警覺,不要氣餒或是過於自滿。透過更有效率的指標來檢視自己的進步程度,例如棒球有很多進階數據,比單純看勝率、打擊率更有意義。
再後面本書就沒有章節了,取而代之的是一些補充、範本、手冊。總之,這本書相當有名,一面講習慣,也一面講目標設定。在這個範疇內,作者已經反覆論證完他的觀點了,是本不錯的書。
[REF]