月份: 九月 2011

前次提到取樣的比例太低時, 樣本誤差需要做修正. 當時的隨機變數是一個數字, 所以它有平均值的概念. 那麼隨機變數如果是一個比例呢? 例如紅豆在八寶粥當中的比例是多少? 所有的紅豆集合起來才能貢獻出一個隨機變數, 因此就沒辦法算出平均值或標準差了.

此時, 我們假設樣本數 n, 樣本中呈現的比率 p, 樣本誤差 D. 那麼在母體當中的比率, 可以用 p ± D 來表示. 而書上說 D = 1.96 x sqrt (p(1-p)/n).

換言之, 若我們舀了一匙的八寶粥, 裡面全都是紅豆, 或是半顆紅豆都沒有; 則 p(1-p) 肯定是 0, 樣本誤差 D = 0. 這表示我們就得相信我們買到的七寶粥 (少了紅豆), 或是一寶粥 (只有紅豆). Well, 這好像是公式的 bug.

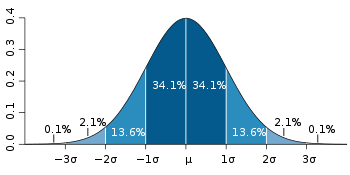
它的理論可以從這裡找到支持. 假設標準差為 µ, 它的平方為變異數 v. 書上說:

換言之, 不要把 p 看做單一的值, 而是一個二值化 (0 or 1) 數列, 一種類型數據, 的平均值的話. (1-p) x p 就像 0 與 1 在對均值 p 計算離均差. 而變異數 v 又是離均方差的平方和的期望值 (平均值). 因此兩者的確很類似.

當然, 上次講到的修正值在比率分析中也是有效的. K = sqrt((N-n)/(N-1), N 表示母體的全部樣本數.

我還漏掉一個東西沒寫, 那就是精確度 (相對誤差), 它等於樣本誤差除以 p (比率) 或是上次的 m (平均值). 個人覺得相對誤差的意義不大, 理論基礎以後再討論.

了解了樣本誤差之後, 當我們再看到政策的支持度由 33%, 降到 27%, 再降到 25% 的時候, 要記得把每個數字都加減樣本誤差, 以得到一個 “母體比率信賴區間".

如果三次民調的信賴區間是重疊的, 那麼我們可以認為三次民調的意義沒有差別. 如果兩次民調和另外一次民調的信賴區間沒有重疊, 那麼它的效力就等於兩次有效的民調. 若三次都沒有重疊, 那麼支持度就真的持續下降了.

以上整理自 “真希望老師這樣教統計".

假設我想知道整家公司的平均體重, 那麼只用一個部門來估計準不準呢? 答案是不準, 因為我們明明知道庶務二課或是秘書課的人都不胖, 所以據此估計出來 “滿帆商事" 的平均體重就會有點誤差. 這不需要數學好就可以知道.

反之, 如果根據一把抓起的豆子重量, 來估計一整桶豆子的重量範圍, 相對就比較準確了.

假設一把抓的豆子總共有 n = 100 顆, 平均數 m = 1g, 標準差 µ = 0.1g. 若整桶豆子約有 N = 10,000 顆, 可計算出樣本誤差 D = 1.96 x µ / sqrt(n) = 1.96 x 0.1 / 10 = 1.96 x 10^-2.

為啥是 x 1.96 呢? 因為假設重量為 N(0,1) 的常態分佈, 在 95% 的範圍內, 標準差為 1.96. 當樣本數很大, 樣本誤差趨近於 0; 反之樣本數為 0 的時候, 樣本誤差趨近於無限大. 如果只有一個樣本, 樣本誤差大約是 2 倍 (1.96 倍) 標準差.

[本圖取自 WIKI 標準差]

換言之, 我們認為那桶豆子的平均重量為 m – D ~ m + D 之間, 也就是 1 – 1.96 x 10^-2 ~1 + 1.96 x 10^-2 或 0.9804~1.0196 g.

或曰, 怎麼和整桶豆子數量級 N 無關? 如果以井觀天, 以蠡測海, 也是用這個公式嗎? 非也, 這時候樣本誤差 D  還要乘上一個修正值 K = sqrt ((N – n) / (N – 1)).

把 D_new 重寫一次得到D_new = 1.96 x µ x K / sqrt (n).

直覺地說, 當 n 趨近於 N, 表示我一把已經把豆子抓光了, 那麼誤差應該修正為 K = 0 與 D_new = 0. 因為 D_new = 1.96 x µ x K / sqrt(n) .

如果真的由井底蛙來估計天空的大小, N >> n 將使得 K = 1. 因此我們知道 K 介於 0~1 之間,

為了抓一個手感, 我們假設 K = 0.49 的話, 則 N – n = 0.7 x (N -1), 0.3N = n – 0.7. 假設 N 和 n 都比較大, 那麼 n > 0.3N 是必須的. 也就是說, 想要讓修正值 K < 0.5, 那麼好歹得一把抓起 3 成的豆豆.   

以上整理自 “真希望老師這樣教統計".

和多變量分析相對的, 是較簡單的單變量分析, 線性迴歸分析即為其中的一種. 假設我們有一群 X 和一群 Y. 而兩者有這樣的線性關係:

Y = a + bX

那麼只要算出 a 和 b, 我們就可以用 X 求 Y, 或是用 Y 求 X 了. 計算 a, b 的步驟如下:

1. 計算 X 與 Y 的平均值 X 和 Y.

2. 計算 X 的離均差平方和. SUM (X_i – X)²

3. 計算 Y 的離均差平方和. SUM (Y_i – Y)²

4. 計算 X 的離均差 x Y 的離均差的和 = 離均差交乘積

SUM ((X_i – X) x (Y_i – Y))

5. 計算

b = 離均差交乘積 / X 的離均差平方和

= SUM ((X_i – X) x (Y_i – Y)) / SUM (X_i – X)²

a = Y – b x X

至於多變量要怎麼分析呢? 最簡單的方式就是用 Excel.

以上摘自 "真希望老師這樣教統計", 作者是菅民郎和土方裕子.

上週去 Costco 的時候剛好看到 “靈劍" (全 3 卷) 和 “天觀雙俠" (全 4 卷), 趁著剛看過 “神偷天下" 的熱情, 就一口氣把鄭丰的全部作品買回來研讀.

正如網路上的評價, “靈劍" 比較難被讀者接受, 但 “天觀雙俠" 確實是一篇罕見的傑作. 鄭丰女士能夠以 “天觀雙俠" 獲得全球華文新武俠小說大賽的首獎, 真的是實至名歸.

這三本作品發表的順序上, 原本和故事發生的順序相反. 不過我既然同時有了這三套書, 正好可以按照故事發生的先後順序來閱讀, 首先是 “神偷天下", 接著是 “靈劍", 最後才是 “天觀雙俠".

靈劍的故事是描述 “正教" 與 “火教" 的對抗史. 這次故事的主角凌霄是一個有特異功能的人, 他可以和動物說話, 又能夠看見別人的未來. 所以咧, 不能接受武俠小說變成神怪小說的人應該沒辦法受得了第一卷的故事.

第一卷故事結束之後, 男主角和對頭 – 火教教主同時失去特異功能. 不過它還是沒有變成一般的武俠小說, 因為作者很明顯地對於篤信宗教卻強烈排它的行為痛加駁斥. 只要把書中的火教教徒口中 “天神" 代換為其他宗教的 “神", 保證那些教徒看得似曾相似, 七竅生煙. 故本書不討喜也是很正常的.

因為這些彆扭的地方, 本書的可讀性的確是低了點. 然而, 把本書當作 “天觀雙俠" 的前傳, 也算是值得一讀了. 這次登場的歷史人物主要是王守仁和寧王. 火教利用寧王造反, 而男主角則協助王陽明平亂. 可惜我看了 “回到明朝當王爺" 之後, 胃口變大了一點. 還挺希望江南四大才子可以在本書登場…, 可惜他們沒出現, 哈!

天觀雙俠的主角是 “靈劍"  男主角凌霄, 男配角成達, 女主角燕龍, 加上反派男主角 – 火教教主段獨聖的下一代.  雙俠的特色是一次寫兩個主角 – 凌昊天 和趙觀. 雖然我先前覺得鄭丰女士在 “神偷天下" 刻劃人物不夠生動. 不過在 “天觀雙俠" 一書中卻大大改觀. 原來她可以一次寫出這麼多有個性的角色. 

這次的故事比較正統, 沒有太奇怪而不能消化的神通和咒術, 主角的蹤跡也東到朝鮮, 西到藏人家, 北到塞外. 連戚繼光, 嚴嵩, 織田信長都編進了小說家言. 其中在提到青幫的時候, 描述的 “切口" 與 “海底" 都活靈活現, 彷彿有青幫的人提供第一手資料. 即使寫得不對都像是真的. 可見作者對這本書相當用心.

據作者在書中的附錄中說的, 她花了八年左右的時間才斷斷續續完成 “天觀雙俠". 原本覺得出版無望, 才會放到網路上供大家欣賞. 想不到 2006 年一舉成名, 獲得極高的評價, 也超出了作者自己的預期. 當然我們希望她愈寫愈好. 既然金庸前輩沒有新作了, 不能讓武俠小說就此走入孤寂才好.