如前面幾篇所寫的, 這是兩位日本人菅民郎和土方裕子, 譯者是李佳蓉小姐.
這本書的開頭相當輕鬆, 比方說它介紹了數據的類型, 哪些是可以統計的, 哪些是不能統計的 (比方血型的平均值).
接著由淺入深, 講到如何統計算標準差, 以及統計中會遇到的誤差. 後面幾章還講到了如何設計與解讀問卷.
以牙醫診所的滿意度為例, 我們可以用問卷問各種問題, 並且計算出一個綜合評價. 假如某個項目的分數與綜合評價的相關係數高, 那麼就表示這個是客戶所特別重視的. 此為分析圖的 X 軸. 而 Y 軸就是各個單項的滿意度.
顯然, 待改進的項目落在右下角的區域. 它與綜合評價相關, 而單項滿意度又偏低.
最後本書教大家用 Excel 實做簡單的統計函數, 以及複雜的多變量分析. 我跟著做了一遍以免以後就懶了~~~ 這本是很不錯的書!
前次提到取樣的比例太低時, 樣本誤差需要做修正. 當時的隨機變數是一個數字, 所以它有平均值的概念. 那麼隨機變數如果是一個比例呢? 例如紅豆在八寶粥當中的比例是多少? 所有的紅豆集合起來才能貢獻出一個隨機變數, 因此就沒辦法算出平均值或標準差了.
此時, 我們假設樣本數 n, 樣本中呈現的比率 p, 樣本誤差 D. 那麼在母體當中的比率, 可以用 p ± D 來表示. 而書上說 D = 1.96 x sqrt (p(1-p)/n).
換言之, 若我們舀了一匙的八寶粥, 裡面全都是紅豆, 或是半顆紅豆都沒有; 則 p(1-p) 肯定是 0, 樣本誤差 D = 0. 這表示我們就得相信我們買到的七寶粥 (少了紅豆), 或是一寶粥 (只有紅豆). Well, 這好像是公式的 bug.
它的理論可以從這裡找到支持. 假設標準差為 µ, 它的平方為變異數 v. 書上說:
換言之, 不要把 p 看做單一的值, 而是一個二值化 (0 or 1) 數列, 一種類型數據, 的平均值的話. (1-p) x p 就像 0 與 1 在對均值 p 計算離均差. 而變異數 v 又是離均方差的平方和的期望值 (平均值). 因此兩者的確很類似.
當然, 上次講到的修正值在比率分析中也是有效的. K = sqrt((N-n)/(N-1), N 表示母體的全部樣本數.
我還漏掉一個東西沒寫, 那就是精確度 (相對誤差), 它等於樣本誤差除以 p (比率) 或是上次的 m (平均值). 個人覺得相對誤差的意義不大, 理論基礎以後再討論.
了解了樣本誤差之後, 當我們再看到政策的支持度由 33%, 降到 27%, 再降到 25% 的時候, 要記得把每個數字都加減樣本誤差, 以得到一個 “母體比率信賴區間".
如果三次民調的信賴區間是重疊的, 那麼我們可以認為三次民調的意義沒有差別. 如果兩次民調和另外一次民調的信賴區間沒有重疊, 那麼它的效力就等於兩次有效的民調. 若三次都沒有重疊, 那麼支持度就真的持續下降了.
以上整理自 “真希望老師這樣教統計".
假設我想知道整家公司的平均體重, 那麼只用一個部門來估計準不準呢? 答案是不準, 因為我們明明知道庶務二課或是秘書課的人都不胖, 所以據此估計出來 “滿帆商事" 的平均體重就會有點誤差. 這不需要數學好就可以知道.
反之, 如果根據一把抓起的豆子重量, 來估計一整桶豆子的重量範圍, 相對就比較準確了.
假設一把抓的豆子總共有 n = 100 顆, 平均數 m = 1g, 標準差 µ = 0.1g. 若整桶豆子約有 N = 10,000 顆, 可計算出樣本誤差 D = 1.96 x µ / sqrt(n) = 1.96 x 0.1 / 10 = 1.96 x 10-2.
為啥是 x 1.96 呢? 因為假設重量為 N(0,1) 的常態分佈, 在 95% 的範圍內, 標準差為 1.96. 當樣本數很大, 樣本誤差趨近於 0; 反之樣本數為 0 的時候, 樣本誤差趨近於無限大. 如果只有一個樣本, 樣本誤差大約是 2 倍 (1.96 倍) 標準差.
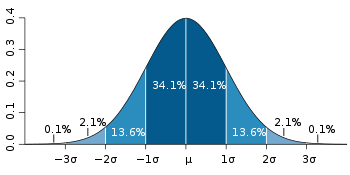
[本圖取自 WIKI 標準差]
換言之, 我們認為那桶豆子的平均重量為 m – D ~ m + D 之間, 也就是 1 – 1.96 x 10-2 ~1 + 1.96 x 10-2 或 0.9804~1.0196 g.
或曰, 怎麼和整桶豆子數量級 N 無關? 如果以井觀天, 以蠡測海, 也是用這個公式嗎? 非也, 這時候樣本誤差 D 還要乘上一個修正值 K = sqrt ((N – n) / (N – 1)).
把 Dnew 重寫一次得到Dnew = 1.96 x µ x K / sqrt (n).
直覺地說, 當 n 趨近於 N, 表示我一把已經把豆子抓光了, 那麼誤差應該修正為 K = 0 與 Dnew = 0. 因為 Dnew = 1.96 x µ x K / sqrt(n) .
如果真的由井底蛙來估計天空的大小, N >> n 將使得 K = 1. 因此我們知道 K 介於 0~1 之間,
為了抓一個手感, 我們假設 K = 0.49 的話, 則 N – n = 0.7 x (N -1), 0.3N = n – 0.7. 假設 N 和 n 都比較大, 那麼 n > 0.3N 是必須的. 也就是說, 想要讓修正值 K < 0.5, 那麼好歹得一把抓起 3 成的豆豆.
以上整理自 “真希望老師這樣教統計".
Cash Chou's Blog 