由於 O(n2) 的 transformer 非常耗能, 後續衍生了諸如 MAMBA 這種 O(nlog(n)) 的技術出來. 與此同時, 巨頭們紛紛蓋起核電廠! 不過等我想到要買 URA, NLR 這類 ETF, 一看都已經溢價 25% 了. 晚了人家好幾步, 根本來不及投資. 那…我再往前亂想好幾步的話還有機會嗎?
我要猜接下來保險業會收到大單, 然後巨頭沒有核電管理經驗, 新手上路, 難免發生一兩個小災變? 接著保險公司調高保費, 趁機大賺一筆. 但投資保險和再保公司又能賺多少? 各國政府用核電廠供 AI 做兵棋推演會買保險嗎? 好像也不會? 何況某些國家都廢核了. 難啊! 總之, 荷馬辛普森, 你不會失業了!
nGPT (Normalized Transformer) [1] 是一種新的節能 transformer, 能夠大量節省計算. 這類演算法由 nVidia 提出也很合理. 因為巨頭們忙著掙錢懶得更新 model, 改變由他們的 vendor 做起, 或許他們可以在不換 vendor 的情況下 silence change?
nGPT 的 n 代表 normalization (均值化), 順便偷渡 nVidia 的 n. 原本在 transformer 裡面有很多個別的 normalization layers. nVidia 的策略就是通通合起來做成灑尿牛丸, 在這顆丸子上, 大家都貢獻一點移動量. (We propose to normalize all vectors forming the embedding dimensions of network matrices to lie on a unit norm hypersphere.) [1]
由 hypersphere 這個名詞得知, 它在一超球體上均值化. 1-sphere 是一個圓, 2-sphere 是一個球, 每個數字都比其維度少 1. hyper-sphere 是某個維度下的所有和中心點等距的點的集合. 雖然論文只用到一個 unit norm hypersphere, 但是其維度是 model 的維度 dmodel, 該 hypersphere 表示為 Rdmodel. 而且既然是 unit norm [-1, 1], 就不會有 weight 衰減的問題 (The normalization renders weight decay unnecessary.) [1]
把參數投到 hypersphere 有啥好處呢? 主要是我們 learning 的時候會根據梯度 (gradient) 方向 update 參數對吧! 如果參數都落在 hypersphere 上, 那麼更新的參數也落在 hypersphere 上, 我們只要用角度就可以表示其移動了, 無論是來自哪一層的貢獻都可以一視同仁.
論文 [1] 提到, 假設有個 a 點要移動到 b 點. 梯度 g = a – b. 則 𝒂 的更新可以表示下面的式子. 其中 α 是介於 0~1 之間權重, 用表示更靠近 a 或是 b. 故它就是 learning rate. 想學的愈快, α 愈接近 1, 新的 a 就愈靠近 b.
| 𝒂←𝒂+α(𝒃−𝒂) 𝒂←𝒂+αg |
根據 Shoemake 的球面線性內差公式 [2], 若 a, b 兩點的夾角 θ=arccos(𝒂⋅𝒃), 給定一個 weighing α ([0:1]), 就能內插出 (最短的) 測地線 (geodesic) 的某個點. 因此前述在平面上的推導, 投影到 hypersphere 上仍然適用.
| SLERP(𝒂,𝒃;α)=sin((1−α)θ) / sin(θ) * 𝒂+sin(αθ) / sin(θ) * 𝒃 SLERP = Spherical Linear Interpolation |
假設原本的 baseline transformer 可以表達為下式.
| 𝒉←𝒉+ATTN(RMSNorm(𝒉)) 𝒉←𝒉+MLP(RMSNorm(𝒉)) |
其中 h = hidden layer 的 state h, RMSNorm = RMS 後做 Normalization, ATTN = attention layer , MLP = multi-layer perceptron = feed forward neural network.
經過 nGPT 的正規化就變成下面的樣子.
| 𝒉←Norm(𝒉+𝜶A(𝒉A−𝒉)) 𝒉←Norm(𝒉+𝜶M(𝒉M−𝒉)) |
其中 Attension 的參數叫做 ATTN(h), 正規化後為 hA = Norm(ATTN(h)) , MLP 的參數叫做 MLP(h) , 正規化後為 hM = Norm(MLP(h)), 它們都可以在這個超球面上計算. 奧妙之處在於 Norm 只剩下一個.
同理它也適用於 optimizer 參數. (以 adam 為例, where 𝜽 is the parameter vector, 𝒈 is the batch gradient, 𝒎 is the momentum, 𝒗 is the estimate of the per-element gradient amplitudes, α is the scheduled learning rate, ϵ is a small constant, and β1<β2 are momentum factors close to 1. ) [1]
表 1 左側的計算, 都變成了右邊 Norm 上面的計算.
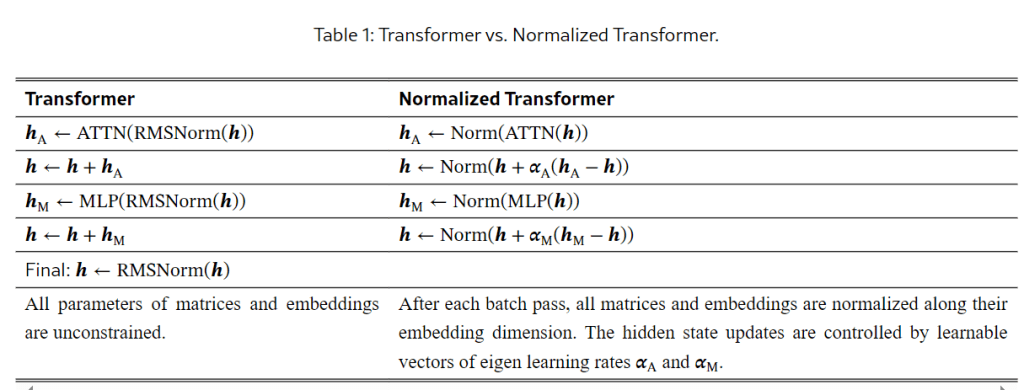
本表取材自 [1].
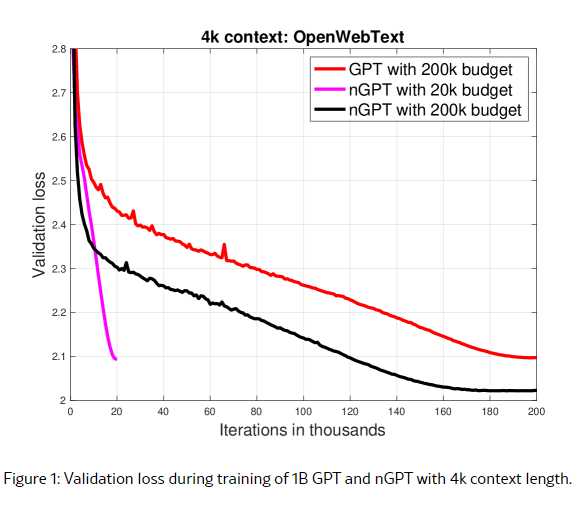
本圖取材自 [1].
總結來說, nGPT 把 baseline Transformer 轉變成 normalized Transformer. 我抓到的重點是:
- 把原本散落各處的 normalization 層都拿掉.
- 對所有的 matrices 都 normalize. 如表 1 所示.
- 把 weight decay 和 learning rate warmup 拿掉.
至於原本論文 [1] 中的 rescale 那些還挺複雜的, 我頭腦不好就跳過了. 總之, 這篇論文提出了一個好主意. 從圖 1 來看, loss 收斂的速度確實也很快.
[REF]
- nGPT: Normalized Transformer with Representation Learning on the Hypersphere
- Animating rotation with quaternion curves.In Proc. of the 12th annual conference on Computer graphics and interactive techniques, 1985.
- 請 Copilot 解說參數同在一個球面的好處.
In NVIDIA’s nGPT, all vectors forming the embeddings, MLP (Multi-Layer Perceptron), attention matrices, and hidden states are unit norm normalized and reside on the same hypersphere. This means that the input stream of tokens travels on the surface of a single hypersphere, with each layer contributing a displacement towards the target output predictions.