馬年快閃電磁學

馬年到了! 和馬有關的成語、吉祥話、成句都紛紛出爐，連馬克斯威爾 (Maxwell) 方程式都出來湊一腳。其它都先不管，講一下和量子力學有關的部分。

第四定律 – “安培-馬克士威定律" 原本長這樣子：

右邊第一項安培定律告訴我們電流 J 流動產生磁場。μ₀ 是真空磁導率。

右邊第二項是馬克斯威爾後來加上去的修正項。意思是：「變化的電場」(E 對時間微分) 也能產生磁場，係數是"真空磁導率" μ₀ 再乘上 “真空電容率" ε₀。

為什麼不用一個 μ₁ 搞定，而要放任 μ₀ ε₀ 存在，增加電信系學生背公式的困難度呢？原因有三個。

1. 增加這兩項的相似性。一看就都是電流家族。
2. 隱藏彩蛋。 μ₀ ε₀ = 1 / C² ，Maxwell 把這兩個係數乘出 μ₁ 的時候，發現他和光速的平方的倒數幾乎一樣。因此他預測了光也是電磁波。However，是說他的計算機有平方鍵和倒數鍵嗎？ 為什麼這樣也能感應到？

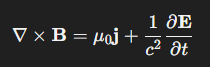
總之，與其用路人般的 μ₁ ，不如寫成光速的平方的倒數更酷。

第三個一點 (教官式中文上身，主要是我不會打清單標題 3)。上述的表示法是國際單位制 (Système International d’Unités，簡稱SI)，便於使用安培、伏特這些單位。假如使用高斯單位制 (Gaussian units) 或 自然單位制，公式就可以直接吸收掉係數 (早說嘛，我大二就可以輕鬆了)，表示為

在量子力學中，甚至把光速視為常數 1，那公式就更簡潔了。

在量子力學中，原本的公式都成立；只是要在量子場論/量子電動力學 (Quantum Electrodynamics, QED) 中重新詮釋。簡單地說，電磁場都不再連續，而是量子態。電與磁對稱，遵守規範對稱性 (Gauge Symmetry) [5]。

跳過不直覺不好記的部分，我們可以簡單記得。馬克斯威爾觀察到 μ₀ ε₀ 參數相乘近似光速的平方的倒數，在忽略量子效應時是對的，但也真的是個近似值。想要精準地推算，就不能忽略量子效應，例如光子的離散性 [6]。

古典世界看起來是連續、對稱的類比，走近一看原來是數位的。我們理解世界的解析度愈低就愈簡單，解析度愈高就會愈覺得 “是這樣沒錯，但不是這樣"。有沒有發現？從蛇年到馬年就是不連續的；所以這又給了我們一次重新立大志做大事的機會。

祝大家蛇年量子跳躍到馬年，別擔心測不準，因為幸福的位置已經塌縮在你身邊！

[REF]

1. 國際單位制
2. 高斯單位制
3. 自然單位制
4. 諧振子
5. 規範場論
6. 光電效應