分類: 筆記

R-Squared 小註解

原本寫完兩篇 R, 就要來寫 R2, 我覺得這個哏不錯! 不過呢, 因為寫著寫著歪樓了, 所以把那邊的主題讓給 P-value, R2 放到後面來.

前面說到 P-value 用來衡量變數的顯著性. 由於我舉的是單一變數的 t-test, 好像 p-value 就足以解釋整個 model. 但真正能解釋整個 model 的是 R2 , 說明如下. 假設:

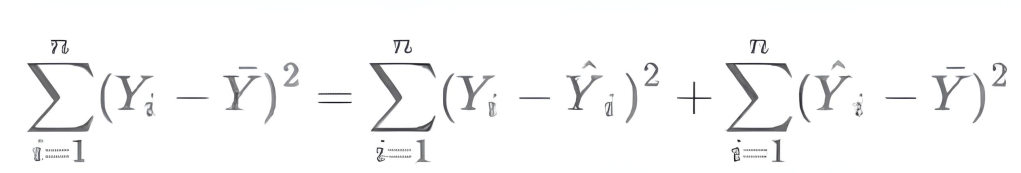
全部的誤差 SST = SSR + SSE .

SSR = residual variation = model 無法解釋的 (實際觀測值 – 模型預測值)

SSE = regression model variation = model 解釋掉的部分 (模型預測值 – y 的平均值)

R2 代表模型解釋變異的能力, 所以是 model 可以解釋的變異的比重 = SSE / SST = 1 – SSR / SST. 所以怎麼看 R 都是介於 0~1 之間. R 越接近 1, 表示 model 解釋得更好.

換個生活化的例子來說明.

  • 假設抽樣調查了三對父子, 記下父親與兒子的身高 (單位:公分):
父親身高 (x)兒子身高 (y)
170172
175177
180179
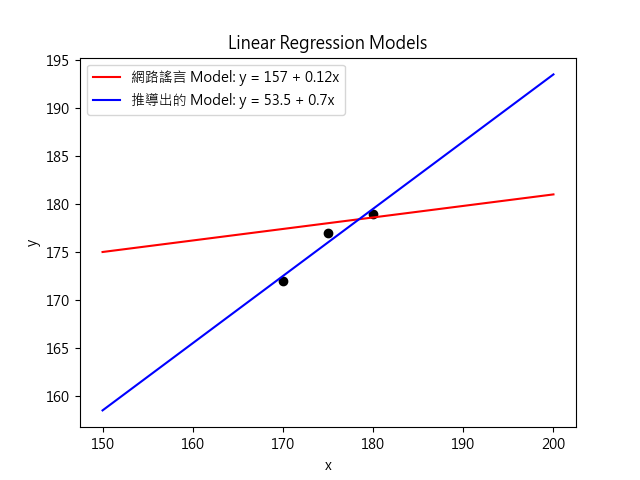
  • 新手根據網路謠言, 建構了下面這個回歸模型:
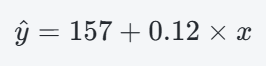
  • 我們來檢驗看看. 首先將每個父親的身高 x 帶入計算, 預測兒子身高 y^.
父親身高 (x)兒子實際身高 (y)預測兒子身高 y^
170172177.4
175177178
180179178.6
  • 計算 R2
  1. 計算 yˉ​= (172+177+179) /3 ​=528/3​ ≈ 176 — 兒子的平均身高
  2. 計算 SST (Sum of squared Total) = (172−176)2 + (177−176)2 + (179−176)2 = (−4)2+(1)2+(3)2=16+1+9=26 — 兒子的身高和平均身高的差的平方和
  3. 計算 SSR (Sum of Squared Residual) = (172-177.4)2 + (177-178)2 + (179-178.6)2 = 29.16+1+0.16=30.32 — 兒子的身高和預測身高的差的平方和

R2 = 1 – SST / SSR = 1 – 30.32 /26 = 1 – 1.166 ≈ -0.166

因為 R2 < 0, 或 SST > SSR, 等於是說: 全部猜平均身高的話, 還比用 model 估來得準. 所以此 model 很不好!

如果我們一項一項分開算. SSE = (177.4−176)2 + (178−176)2 + (178.6−176)2 = 1+4+6.76 = 12.72

SST ≠ SSR + SSE 或 26 ≠30.32 + 12.72

為何會有這樣的結果呢? 主要是這個 model 不正確, 所以什麼都解釋不了. 發生這種問題可能的原因包括:

  • 模型套錯：使用的模型和資料的型態根本不吻合（例如線性模型去解釋非線性資料）
  • 資料點太少：樣本數極少，容易受到極端值影響
  • 預測變數選錯：所用的 x、公式、或回歸參數明顯偏離資料特性
  • 資料雜訊過高：資料本身的變異無法用簡單模型捕捉

讓我們只用這三筆資料來生成合理的 linear regression model, 並重新計算 R2. 這個部分就請 AI 來執行了.

1. 原始資料
父親身高 (xx)兒子身高 (yy)
170172
175177
180179
2. 計算步驟
步驟一：計算平均值
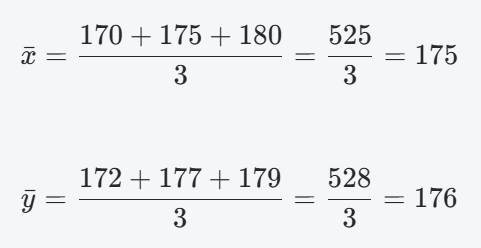
步驟二：計算斜率 (b)


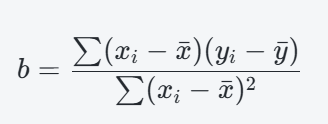
b=0.7

步驟三：計算截距 (a)

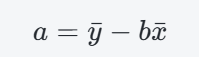
a=53.5

3. 生成線性回歸方程式

​解釋為: 父親每增加 1 公分身高, 兒子的預測身高增加 0.7 公分.

4 . 重新計算 R2

這個新模型不就超準了嗎? 但我們這裡只是建立 model, 並且評估其效果. 還不可以把它視為真正能實用. 下圖可以看到網路謠言版和依照數學原理建立的 model 有何差異? 網路謠言 model 不能解釋我們的資料庫, 但實測會不會更好? 這件事無法反映得出來.

T-Test 和 P-Value

雖然今天有望創下投資市值新高 (舊紀錄是 2025/2/20) – 台股平平、日股創高、美股小漲還沒收市, 結果還不好說 . 但這篇的重點是整理上班會用到的一門統計技術.

假設我有大把的 features, 要怎麼知道每個因子對 model 有沒有影響? 以及因子之間是否過於相關 (例如華氏度和攝氏度) 而顯得多餘呢? 讓我們從基本問題開始理解.

首先我們會遇到每個因子的 scale 差異很大. 例如預測房價時, 我們可能有屋齡、坪數、坪單價、附近實價登錄總價等因子. 前兩個算它們從 0~1,000 應該就夠用. 甚至普通人應該不會買千坪豪宅、千年老宅 (古剎?). 至於後兩個就有趣了. 假設我們用萬元為單位, 那麼 後兩者的 order 可能差個 10 倍到上百倍 (10~100 坪), 更不用說和前兩個因子擺在一起比較, 總會有些因子顯得參差不齊~~~

甚至那些 one hot encoding 來的, 根本就是單位向量, 這時要怎麼辦呢? 我們可以對 skewed 的變數取對數 log, 或用標準化 (z-score) 將所有因子拉到類似範圍。這類轉換能處理加法和乘法效應的混合 [1]，讓模型更公平. 這部分先帶過, 減少數學、訴求直覺就好.

接下來要篩選出有用的因子, 把雜質打掉, 才能真正抓到關聯性. 我們要先檢查因子之間的相關性 (避免如華氏/攝氏度的多餘), 並確保數據的有效性. 如果數據本身沒意義, 其他動作都是多餘的.

以下就介紹 t-test 和 p-value：它們是用來測試每個因子是否真的對目標變數 (如房價) 有顯著影響. 簡單說, t-test 測量因子的 “效果強度", p-value 則告訴你這種效果在隨機情況下發生的機率有多高— p 小表示影響顯著！

顯然, 我們要做一些測試才會產生測量因子. 假設我們用了單樣本測試 (One-sample t-test), t 公式表示如下 (t 公式還有很多型態).

例如測試新藥是否使血壓平均降至 120 mmHg, 多筆測量出的血壓為 x, 假設值 μ0 為吃了藥但無效果的血壓 (虛無假設), 此時可以看出 x 的平均值 xˉ 並不是 μ0. 假設此藥對某人藥效不佳, 吃了高血壓藥, 收縮壓從 140 變成 150, 差異是 +10, 或是對某人藥效太強, 收縮壓從 135 變成 90, 差異就是 -45.

  • 假設資料（血壓變化值，單位 mmHg）：
    • 受試者 1: -5（血壓下降 5）
    • 受試者 2: -3
    • 受試者 3: -7
    • 受試者 4: -4
    • 受試者 5: -6
    • 樣本平均 xˉ=−5xˉ=−5（整體平均下降 5 mmHg）
    • 樣本標準差 s ≈ 1.58
    • 樣本大小 n = 5
    • 虛無假設 μ₀ = 0（藥物無效果）

此時 t = (-5-0)/(1.58 / √5)=-5/​0.707≈−7.07,

t 可以表示出藥效過高或試過低. 由於 t 就是一個正規化的過程. 所以 x 不需要預先做正規化處理.

另外還有個 p-value, 它的計算不是公式, 而是機率的累積函數 CDF (cumulative distribution function). 再以血壓藥為例, p 是紅線以下的面積 + 右邊對稱位置的面積 (所以 x2).

p=2×(1−CDFt​(∣−7.07∣,df=4)) = 0.0021

也就是在自由度 [2] df = n – 1 = 5 – 1 = 4 的情況下, 落在分布長尾部分的機率 (tail probability).

用實際的數字翻譯上述公式就是: t ≈ -7.07, df=4, p ≈ 0.0021 解釋為: 如果藥物無效（H0:μ=0），則發生五個受試者 t = -7.07 或更極端 (更負或更正) 的機率只有 0.2%. 隱含這種事不太可能發生, 藥物相當可能是有效的.

換個角度, 如果大家試完藥, t -> 0, 測起來像是這個藥吃了沒效. 但 p -> 1 只是表示這個測試的證據力很低, 表示無法證明這個藥有效, 而不是證明這個藥非常無效.

[REF]

  1. http://ch.whu.edu.cn/cn/article/doi/10.13203/j.whugis20210659?viewType=SUP
  2. 自由度 – 在計算樣本標準差（s）時，我們先用樣本平均值 (xˉ) 來「約束」資料: 一旦知道平均值, 前 n-1 個值可以自由變化, 但最後一個值必須調整以符合平均值. 這 “犧牲" 了 1 個自由度. 當自由度愈低, 表示愈不確定, 長尾就比較肥. 對同一個 t, p-value 相對大.

利率公式小整理

自從川普 2.0 之後, 讓我想要惡補一下財經這個領域. 回想起當時亂花的錢, 流失的歲月和破碎的記憶. 先來複習十六年前讀過的東西好了.

[常用縮寫]

  • T = numbers of annuity payments
  • r = the interest rate
  • g = growing rate
  • Po = Present value of annuity
  • PMT = Payment
  • A = annuity payment
  • PT = Expected future value of investment
  • n = number of compounding periods
  • FV = Future value of an annuity
  • PV = Present value of cash flows

[基本公式]

PT = Po(1 + r)T

Po = PT(1 + r)-T

  • if Perpetuities, T ->∞,

Po = (A/r) (1-(1 + r)-T) = A/r

[縮寫公式]

Annual Compound Factor = ACF(r, n) = [(1+r)n −1]/r

Annual Discount Factor = ADF(r, n) = (1−(1+r)-n)/r

[分期付款]

貸款金額的複利本利和 = 每月還款金額的 ACF,

假設貸款 100 萬, 每個月還 1 萬, 一共還 10 年, 共 120 期.

理解為現在的 100 萬, 放著會生利息, 最後得到 Fv. 由貸款人每個月 PMT 的 ACF 償還.

100 * (1+r)120 = ACF(r, 120) = [(1+r)120 −1]/r

100 = [1-(1+r)-120 ]/r

PV = PMT * [1-(1+r)-n ]/r

[不斷配息的股票]

有個股票, 每年無止盡地配息 100 元, 堪比永動機, 股價為何不是無限大?

Perpetuity is a series of equal payments of a fixed amount for an
infinite number of periods.

  • if Perpetuities, T ->∞,

Po = (A/r) (1-(1 + r)-T) = A/r

假設機會成本為 5%, 該股票只值 2,000 元.

[利息成長的股票] (Growing Anuity)

假設這個股票不只是每年配息 A, 利率 r, 還會以 g 的比例成長, 那價值應該更高了吧!

第一年, 配息 A

第二年, 配息成長為 A(1+g)

第 n 年, 配息成長為 A(1+g)n-1, 折現為 A(1+g)n-1 / (1+r)n

將無限多年的折現現金流加起來:

PV = ∑ｔ=1∞ ​A(1+g)ｔ−1​ / (1+r)ｔ

把 １+r 和 1+g 的指數弄成一樣 PV = A / (1+r) * ∑ｔ=1∞ ​((1+g) / (1+r))ｔ-1

因為 ∑ｔ=0∞ ​xｔ=1 / (1−x) 當 ​∣x∣<1. 也就是末項趨近於 0, 首項為 1 的等比級數公式特例.

其中, 乘號左邊為 A / (1+r), 右邊為 1 / (1-x), 其中 x = (1+g)/ (1+r)

右邊 = 1 /( (1+r-1-g)/ (1+r)) = 1 /( (r-g)/ (1+r)) = (1+r) / ( r-g)

PV = (A / (1+r)) * (1+r)/ (r-g) = A / (r-g)

當然 r > g 的時候本公式都符合直覺. 忘掉一切, 只記得 A / (r-g) 就好.

[利息成長的縮寫公式]

Annual Discount Factor = ADF(r, n, g) = 上面沒投機化簡的 PV = A / (1+r) * ∑t=1n ​((1+g)/ (1+r))t-1 ,

老老實實地按等比級數求和展開, 乘號右邊 ∑t=1n ​((1+g)/ (1+r))t-1 = 1-(1+g)/ (1+r))n / ( 1- ​((1+g)/ (1+r)))

PV = A / (r-g) *(1- ((1+r)/(1+g)) n-1)

同樣的思路可以推導出, ACF (r.n.g) = A/(r-g) * ((1+r)n – (1+g)n)

以前除了手算, 考試可以用財務計算機. 我手上的 TI BA II Plus 已經沒電了, 但沒有換電池的必要, 現在有 Excel 處理這些東西, 更可以無腦問 AI. 不過呢, 直覺是慢慢培養起來的, 一直問 AI, 自己沒辦法產生敏銳度~~~

2024 年重點回顧

雖然這件事應該是昨天以前要做的, 即使我遲交了, 還是值得做個結語.

  1. 年初學了如何用 Python 處理 Excel 表格, 這個工作上用來統計 task weighting 很方便.
  2. 考慮未來是 AI 的時代, 整年到處上課和看展, 最辛苦的是拿到一張 TensorFlow Developer 證書. 畢竟老人只能說一嘴好 AI 的話, 那就沒有啥說服力。
  3. 考慮到數據中心很重要, 我想知道它跟 AI 是什麼關係？於是做了點研究， 還拿了一張 Google Cloud 的Machine Leaning Engineer 證書.

4. 至於最花錢的課莫過於這個. 在 Amazon Skill builder 一個月花了 905.21 美金. 其實只跑了兩個 model. 因為菜鳥不懂得用完要下線, 下一個月又白白被多 charge 一次. 真是花錢如流水~~~

5. 年中老闆說部門缺專利, 我一口氣申請了 7 個. 本來想湊十個, 不過部門目標已經達成了。考慮到邊際效益遞減，我還是把腦力保留到 2025, 不需要做無效的攻擊. 整年共獲得 10 個專利, 台灣新增 6 個, 美國 2 個, 大陸 2 個. 當然這些是前幾年申請的.

6. 出差去印度, 解鎖了一個我旅行清單中偏難的項目。可惜出差行程不可能看到什麼大景, 就是到此一遊。主要亮點還是和家人去了日本和土耳其. 家庭旅遊的部份 pilot run了 “帶家人坐商務艙到處去旅行" 的願望. 重點是這年可以完全丟下小孩, 因為她自己跑去澳洲打工度假了.

2024 年都在學技術, 沒讀到幾本書. 本來說要學英日文都沒進展, 說要減重還胖了!? 這、這是冬天的關係吧! I hope so. 總之, 2024 學了一些新知識. 2025 年希望學更多知識, 也希望跟工作做更多結合.

去年年底網路上很多人 po 文說 2025 =452, 所以這是很特別的一年. 同學還找了更多組合, 像是 (1+2+3+4+5+6+7+8+9)2 = 2025 之類. 其實根本就同一件事. 既然如此, 那今年就是海綿寶寶年了! 讓我們用海綿寶寶考駕照的精神迎接一整年的挑戰吧! 诶? 不對! 他好像一直沒考上耶!? 忘掉駕照, 我們學習他的樂觀就好了. 加油!

少年 Py 的奇幻漂流

週日晚上做了一個夢。有位老先生用毛筆字寫了封信給我，署名林如松，要我照顧他的兒子。說這個兒子學習不好是因為某種心理疾病吧！總之懇請多多照顧等有上百來字。望文生義，那麼我在夢中的身份就是個導師了。

身為導師, 而不是醫師。我開始找醫學相關的線索。在一張可能是精神科醫師的桌子上，我發現了名片。上面寫了幾個小字說明醫師的專業。細節忘了，但其中 “止冰" 兩個字清楚地印入我的眼簾。這是什麼? 要阻止冰塊? 還是冰毒? 我納悶了一會兒，才恍然大悟是"治病" 的諧音.

病人因為精神疾病來求診，有點害羞會不想讓人知道，所以醫師就用某某人止冰來隱晦這件事! 想不到我只是做個夢，也會自編自導諧音梗啊! 在我破解了自己的梗之後，空中又傳來一個自問自答。"為什麼脖子太長不好? " 隔了一下，"因為好"頸" (景) 不長 (常)"。看來我的夢境是進入了諧音梗的 decorator [1].

等等! 一開始我有正經任務的啊! 怎麼跑題了? 想到這裡，世界又變得緊張嚴肅了。好像是初三23:59’57″ – 快初四 (出事)了! 我帶著兩三個人開始闖關，其中也不知道有沒有包括林小弟? 總之系統瞬間提示倒數 3 秒鐘，如果不在限時內讓機關套住一個掛勾，在我後面的人都會從平台上滑下去。正當我回頭叫其他人跟上來，倒數 3 秒已經 “加速" 結束了。我能跟大家說的話只有 一句 “來不及了"。

然而，即使倒數時間到了，我沒有完成任務，其他人也沒跟上，但好像並沒有發生什麼了不起的事? What not happened? 難道因為我們的 3 秒不是真的 3 秒，Dead line 也就不是 line 了嗎 ? 換言之，line 變成 non-linear，所以 dead 也就不 dead 了 !? 這麼一想好像也有道理。好比 nonlocal [2] 如字面所說，雖然不是 global，但肯定不是 local。事前有舖梗，後面就拗得過去。

看來這個夢中世界的 “人設" 很不靠譜啊!? 果然畫面再一轉，出現了那位忘記是自稱還是人稱喇賽之王的前同事 “肯"， 帶著我們一行人小跑步穿越著商店街。沒有要 shopping，就是路過著日常騎樓下攤販。本來好像要堂堂展開的華麗冒險，就這樣被 apply(荒謬且搞笑) [3] 了.

Anyway，不管發生什麼事，我們都可以正向解讀。其實我們這位前同事去了谷歌。也許我祖先周公暗示著不管局勢多麼奇幻，還是要好好探索 (Google) 一下未知的領域。那些小攤位就不逛了，我們繼續前行，找出更重要的線索。既解決林小弟的困擾，幫助那位老林先生，同時也完成自己的任務。

[REF]

1. 在 Python 中，裝飾器（decorator） 的作用是用來修改或增強函數的行為。當你使用裝飾器時，原函數會被包裝到一個新的函數（通常是內部的 wrapper_func）中，因此裝飾器會影響函數的執行方式。例如: 

      from datetime import datetime

def 計時器(func):
    def wrapper():
        現在時間 = datetime.now()
        小時 = 現在時間.hour
        print (小時, "點了")
        func()
    return wrapper

@計時器
def 打招呼():
    print("你好！")

打招呼()

      2. 在 Python 中，nonlocal 關鍵字用於在嵌套函數中聲明變數，讓內層函數可以修改外層（但非全局）作用域中的變數。

      def 按讚():
    
    次數 = 0
 
    def comment_filter(好評):
        nonlocal 次數

        總類 = ["讚", "愛心", "加油"]
        if 好評 in 總類:
            次數 +=1

        print(f"好評 {次數}")
    return comment_filter

按 = 按讚()
按("哭")
按("愛心")

      3. .apply() 主要在 Pandas 中使用，是一個非常強大的函數，用於對 DataFrame 或 Series 進行數據處理。例如: df[‘成績’].apply(加分)

      import pandas as pd
import math

data = {
    '姓名': ['林明明', '李大同', '王小美'],
    '成績': [85, 92, 5]
}

def 加分(row):
    # 取得成績值
    score = row['成績']
    # 計算新成績
    new_score = math.sqrt(score) * 10
    return new_score

# 建立 DataFrame
df = pd.DataFrame(data)

# 使用 apply 並傳遞整個 DataFrame
df['新成績'] = df.apply(加分, axis=1) 

print("DataFrame 內容：")
print(df)