雖然今天有望創下投資市值新高 (舊紀錄是 2025/2/20) – 台股平平、日股創高、美股小漲還沒收市, 結果還不好說 . 但這篇的重點是整理上班會用到的一門統計技術.
假設我有大把的 features, 要怎麼知道每個因子對 model 有沒有影響? 以及因子之間是否過於相關 (例如華氏度和攝氏度) 而顯得多餘呢? 讓我們從基本問題開始理解.
首先我們會遇到每個因子的 scale 差異很大. 例如預測房價時, 我們可能有屋齡、坪數、坪單價、附近實價登錄總價等因子. 前兩個算它們從 0~1,000 應該就夠用. 甚至普通人應該不會買千坪豪宅、千年老宅 (古剎?). 至於後兩個就有趣了. 假設我們用萬元為單位, 那麼 後兩者的 order 可能差個 10 倍到上百倍 (10~100 坪), 更不用說和前兩個因子擺在一起比較, 總會有些因子顯得參差不齊~~~
甚至那些 one hot encoding 來的, 根本就是單位向量, 這時要怎麼辦呢? 我們可以對 skewed 的變數取對數 log, 或用標準化 (z-score) 將所有因子拉到類似範圍。這類轉換能處理加法和乘法效應的混合 [1],讓模型更公平. 這部分先帶過, 減少數學、訴求直覺就好.
接下來要篩選出有用的因子, 把雜質打掉, 才能真正抓到關聯性. 我們要先檢查因子之間的相關性 (避免如華氏/攝氏度的多餘), 並確保數據的有效性. 如果數據本身沒意義, 其他動作都是多餘的.
以下就介紹 t-test 和 p-value:它們是用來測試每個因子是否真的對目標變數 (如房價) 有顯著影響. 簡單說, t-test 測量因子的 “效果強度", p-value 則告訴你這種效果在隨機情況下發生的機率有多高— p 小表示影響顯著!
顯然, 我們要做一些測試才會產生測量因子. 假設我們用了單樣本測試 (One-sample t-test), t 公式表示如下 (t 公式還有很多型態).

例如測試新藥是否使血壓平均降至 120 mmHg, 多筆測量出的血壓為 x, 假設值 μ0 為吃了藥但無效果的血壓 (虛無假設), 此時可以看出 x 的平均值 xˉ 並不是 μ0. 假設此藥對某人藥效不佳, 吃了高血壓藥, 收縮壓從 140 變成 150, 差異是 +10, 或是對某人藥效太強, 收縮壓從 135 變成 90, 差異就是 -45.
- 假設資料(血壓變化值,單位 mmHg):
- 受試者 1: -5(血壓下降 5)
- 受試者 2: -3
- 受試者 3: -7
- 受試者 4: -4
- 受試者 5: -6
- 樣本平均 xˉ=−5xˉ=−5(整體平均下降 5 mmHg)
- 樣本標準差 s ≈ 1.58
- 樣本大小 n = 5
- 虛無假設 μ₀ = 0(藥物無效果)
此時 t = (-5-0)/(1.58 / √5)=-5/0.707≈−7.07,
t 可以表示出藥效過高或試過低. 由於 t 就是一個正規化的過程. 所以 x 不需要預先做正規化處理.
另外還有個 p-value, 它的計算不是公式, 而是機率的累積函數 CDF (cumulative distribution function). 再以血壓藥為例, p 是紅線以下的面積 + 右邊對稱位置的面積 (所以 x2).
p=2×(1−CDFt(∣−7.07∣,df=4)) = 0.0021

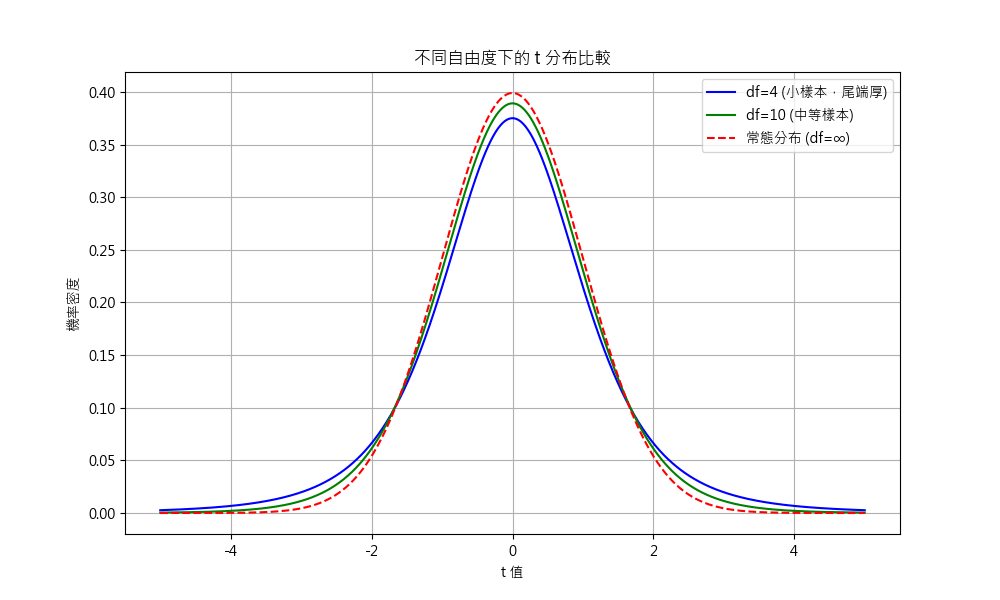
也就是在自由度 [2] df = n – 1 = 5 – 1 = 4 的情況下, 落在分布長尾部分的機率 (tail probability).
用實際的數字翻譯上述公式就是: t ≈ -7.07, df=4, p ≈ 0.0021 解釋為: 如果藥物無效(H0:μ=0),則發生五個受試者 t = -7.07 或更極端 (更負或更正) 的機率只有 0.2%. 隱含這種事不太可能發生, 藥物相當可能是有效的.
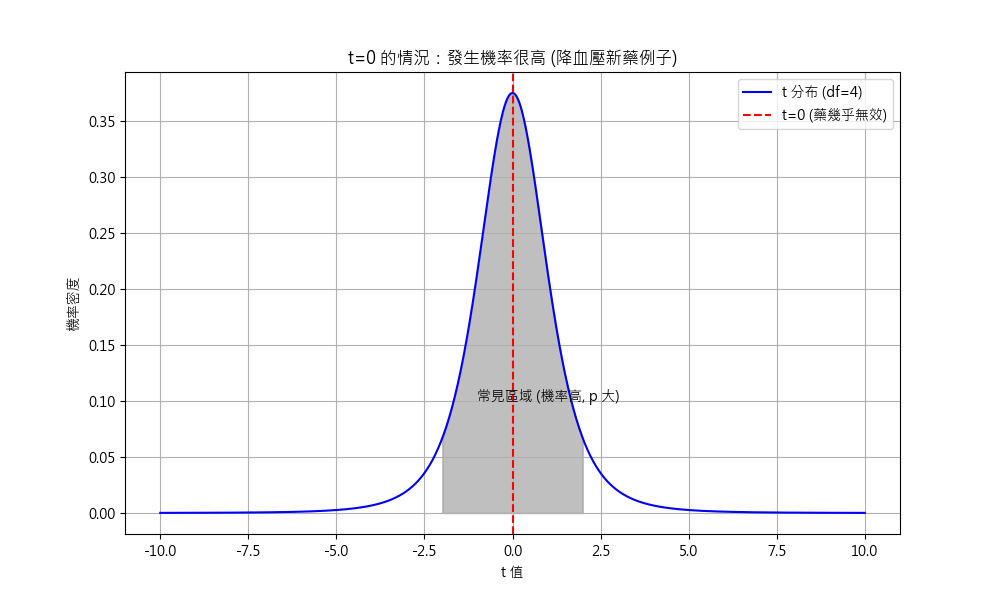
換個角度, 如果大家試完藥, t -> 0, 測起來像是這個藥吃了沒效. 但 p -> 1 只是表示這個測試的證據力很低, 表示無法證明這個藥有效, 而不是證明這個藥非常無效.
[REF]
- http://ch.whu.edu.cn/cn/article/doi/10.13203/j.whugis20210659?viewType=SUP
- 自由度 – 在計算樣本標準差(s)時,我們先用樣本平均值 (xˉ) 來「約束」資料: 一旦知道平均值, 前 n-1 個值可以自由變化, 但最後一個值必須調整以符合平均值. 這 “犧牲" 了 1 個自由度. 當自由度愈低, 表示愈不確定, 長尾就比較肥. 對同一個 t, p-value 相對大.